Visitors Counter
7758 visitors since Jan 2010
All pictures from Acheron 2.0
|
|
Introduction Back to Top
The euclidean geometry uses objects that have integer topological dimensions. A line or a curve is an object that have a topological dimension of one while a surface is described as an object with two topological dimensions and a cuve as an object with three dimensions. This geometry adequately describes the regular objects but failed to be applicable when it comes to consider natural irregular shapes.
Benoit B. Mandelbrot introduced a new concepts, that he called fractals, that are useful to describe natural shapes as islands, clouds, landscapes or other fragmented structures. According to Mandelbrot, the term fractals is derived from the latin adjective fractus meaning fragmented. According to Mandelbrot, a fractal can be defined as 'a set for which the Hausdorff-Besicovitch dimension strictly exceeds the topological dimension'. This clever mathematical definition, albeit quite obscure for non-initiated people, means that a fractal curve is a mathematical
function that produce an image having a topological dimension between one and two. Intuitively, fractals can be seen as curves partially filling a two-dimentional area. These curves are often described as space-filling curves.
Fractals curves exhibit a very interesting property known as self-similarity. If you observe precisely the details of a fractal curve, it appears that a portion of the curve replicates exactly the whole curve but on a different scale. Mathematicians have in fact created geometrical fractal curves long before the introduction of the fractal geometry by Benoit Mandelbrot. Some
of these curves are well-known as the Von Koch's snowflake or the triangle of Sierpinsky.
| |
 |
|
The american physicist John Heighway discovered this curve while working at
NASA. The Heighway curve, also called the Heighway Dragon or Harter-Heighway Dragon, was popularized in 1967 when Martin Gardner described it in American Scientific. Three years later, the first mathematical analysis was published by Chandler Davis and Donald Knuth. Although the construction of this curve is
quite simple, its fascinating properties have stimulate a lot of works in different fields of mathematics. |
|
Construction Back to Top
While three methods were described for the construction of the Dragon
curve, the discussion will be limited to the method used originally by
Heighway.
To construct the curve, imagine that you take a trip of paper. Fold it in
two equal parts by taking the right edge and adjusting it above the left edge
of the trip. Repeat this operation two or three times and then unravel the paper
trip so that each corner makes a right angle in the natural direction of the
fold. Looking at the paper trip from the edge will reveal the Heighway curve.
Here are the result of the first five foldings:
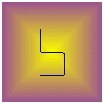
Note that the software strips slightly the folding corners to avoid
touches between folders.
Increasing the number of folding leads to more and more complex drawing
and, finally, to the limiting shape, the Dragon Curve.
There are two types of folding: the folding of type 1 consists of ajusting
the right edge above the left edge of the paper. The folding of type 0
is the inverse operation, as you adjust the right edge below the left
one.
Mixing folding types changes dramatically the look of the curve:
Folding 11111111 ( 8 foldings of type 1)
Folding 10101010 ( 8 foldings alternatively of type 1 and 0)
Folding 11100111 ( 6 foldings type 1 with 2 of type 0 in the middle)
Playing around with the folding sequence may lead to very peculiar drawings ...
Properties Back to Top
- Curve Order
This property derives from the construction method: a curve of order n is
the combination of two curves of order n - 1.
As an example, the following picture shows:
- on the left, a curve obtained by using the folding sequence 111111
- on the right, two instances of a curve obtained with a 11111 sequence, one
of them being rotated to be in the correct alignment.
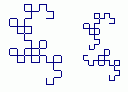
- Fractal Dimension
The fractal dimension is computed using the
Hausdorff-Besicovitch equation:
D = log (N) / log ( r)
The self-similarity N and r values are derived from the construction of
the curve using the triangle method.
D = log(2) / log(2*sqr(2)) = 2
Variations Back to Top
All Variations described are available using Acheron 2.0
- Folding Sequence
The folding sequence is entered as a string of 1 and 0, up to 16 characters.
Author Biography Back to Top
|
|
|
