The Squares curve is a nice fractal curve, build using a recursive procedure. I saw a sample of this curve in the well-known book 'Algorithms in C' written by Robert Sedgewick (Addison-Wesley Publ. ISBN 0-201-51425-7). It was not named from its inventor so I call it the Squares Curve. As almost all the geometric fractal curves, this curve shares the fascinating property of having an infinite curve length in a finite area.
All pictures are from Acheron 2.0, a free explorer of geometrical fractals. You can download Acheron 2.0 here
Construction Back to Top
The starting point of the recursive method for drawing the Squares curve is
a simple square.
Use the four corners of the square as the center of 4 smallers squares,
each having half the size of the main square. The first iteration gives:
The same procedure gives already a nice picture at the second iteration:
Properties Back to Top
- Curve Length
- Curve Area
- Fractal Dimension
- Self-Similarity
The following reasoning concerns the curve for which only the outline is drawn. This gives a close curve with an univocal perimeter.
Take the initial square and name N the length of its side. The perimeter of the 'curve' is N * 4.
On the first iteration, the four corners are replaced by four smaller squares. So, the length of the curve is now equal to the sum of the segments common between recursion 0 (initial square) and recursion 1 plus the length of the newly added segments. The total length of the two segments removed at each corner is N/2, so the total removed is (N/2) * 4. The total length of the segments making the smaller squares is N/2 * 3 and 4 are added, one on each corner. Looking only at the added segments, the length increase is:
Linc = (N/2)*3*4 - (N/2)*4 = (N/2)*8
On the second iteration, the four small squares added at the first iteration will be replaced by four smaller squares. Here, the length of the segments removed on each square corner is equal to N/4 and the length of the smaller squares added is equal to (N/4) * 3. Looking only at the added segments, the length increase is:
Linc = (N/4)*3*3*4 - (N/4)*3*4 = (N/4)*24
The formula for the length increase can be generalized as:
Linc = (N/2Rec) * 8 * 3(Rec - 1)
where Rec is the iteration number (starting at 0)
Here is a summary of the length increase and total length of the curve.
| Iteration Number | Length Increase | Total Length | |
|---|---|---|---|
| 0 | ... | ... | N * 4 |
| 1 | (N/2) * 8 | N * 4 | N * 8 |
| 2 | (N/4) * 24 | N * 6 | N * 14 |
| 3 | (N/8) * 72 | N * 9 | vN * 23 |
| 4 | (N/16) * 216 | N * 13.5 | N * 36.5 |
| 5 | (N/32) * 648 | N * 20.25 | N * 56.75 |
The Ratio of the length increase between two successive iterations is:
Ratio = ((N/2(Rec+1)) * 8 * 3Rec) / ((N/2Rec) * 8 * 3(Rec-1))
Solving the equation gives Ratioinc = 1.5, demonstrating what is quite obvious from the figures in the above table.
The formula of the length increase can then be generalized to:
Linc = N * 4 * rRec-1 where r = 1.5
The total length of the curve is equal to the original length plus the sum of all the length increases.
Using the following identitiy,
1 + x + x2 + x3 + ... + xn = (xn+1 - 1) / (x - 1)
the total length can be generalized:
LTot = N * (( rRec * 8) - 4)
Graphically, it gives a nice view of the ever increasing length: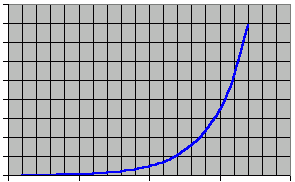
Take the initial square and name N the length of its side. The area of the 'curve' is noted N2. Using a reasoning analogous to the one followed for the determination of the curve length, the formula for the curve area is obtained.
The area increase at each iteration can be generalized as:
Areainc = (4 * 3Rec) / 4Rec+1
Solving for the Ratio of the area increase between two successive iterations gives: Ratio = rRec where r = 0.75
The total area of the curve can then be expressed as:
AreaTot = N2 + ( 1 + rRec + r(Rec+1) + .. r(Rec+n))
Using the following identitiy,
1 + x + x2 + x3 + ... + xn = (xn+1 - 1) / (x - 1)
the total area can be generalized:
AreaTot = N2 * 4 * ( 1 - rRec+1)
As rRec+1 tends to Zero when iteration increases, the area tends to 4 times its original value.
Graphically, it gives a nice view of the finite area: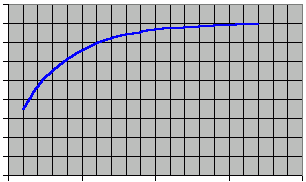
The fractal dimension is computed using the Box-Couting Method equation:
D = log (N) / log ( r)
The following picture helps finding the figures required by the formula:
Replacing r by 14 ( as the grid is 14 * 14) and N by 148 ( the number of small squares covered by the fractal curve) in the the Box-Counting equation gives:
D = log(148) / log(14) = 1.89356
Looking at two successive iterations of the drawing process provides graphical evidence that this property is also shared by this curve.
All Variations described are available using Acheron 2.0
- Iteration Level
- Curve Style
- Normal
- Filled
- Outline
Eight recursion levels are available. Above this iteration number, the overall aspect of the curve remains essentially unaffected.
Three ways for rendering the curve are available:
Born: 20 Dec 1946 in Willimantic, Connecticut, United StatesRobert Sedgewick was born in Willimantic, Connecticut where his parents were professors at the University of Connecticut. He earned a bachelor of Science (1968), a master in applied mathematics (1969) and received his PhD at the Stanfaord University (1975). He developped lot of algorithms and wrote 20 books covering different languages (C, C++, java) tranaslated all around the world.
Complte biography avaiable on Wikipedia